목표
1. 모집단과 표본 / 샘플링
모집단(Population)
통계를 통해 알고 싶어하는 군단
모집단의 특정(모수 : parameter) - 모평균, 모분산, 모표준편차 등
표본(Sample)
모집단의 분포, 특성을 알기 위해 모집단에서 추출된 일부 집단
표본의 특성(통계량 : statistic) - 표본평균, 표본분산, 표본표준편차 등
추출(Sampling)
모집단에서 표본을 추출하는 방법
추출 방법 :
- 단순 샘플링(랜덤 샘플 추출)
- 층화 샘플링(모집단을 그룹으로 나눠서 각 그룹에 랜덤하게 몇몇을 뽑는 형식)
- 계통 샘플링(모집단 데이터에 1~n 번호를 붙여서 일정 간격별로 데이터를 추출하는 방법)
- 군집샘플링(모집단을 군집으로 여러개 나누고 여러개의 군집중 몇몇개만 뽑아서 데이터로 사용한다)
추론(inference)
표본 통계량으로 모집단의 특성을 추론한다
2. 정규 분포와 중심 극한 정리
정규 분포
연속 활률 분포중에서 가장 많이 사용
평균에 대해서 좌우 대칭, 평균에서 최대값을 가지고 종모양이다
정규 분포는 평균(노란선), 표준편차(빨간 물결)에 의해 결정된다.

중심 극한 정리
표본의 크기가 커질수록 표본 평군의 분포는 모집단의 분포 모양과는 관계없이 정규 분포에 가까워진다.

3. 카이제곱분포
- 카이제곱 분포의 자유도가 높을 수록 정규 분포에 근점
- y축에 편향된 분포
- 제곱된 분산값을 다루기 때문에 음수가 없다

4. 스튜던트 t분포
- 모분산이 알려져 있지 않고, 소규모 표본인 경우에 새로운 분포를 개발
- 정규 분포와 생김새가 비슷하나, 꼬리 부분이 두껍다
- 표본의 크기가 30이하인 경우, t 분포를 사용한다.

5. F 분포
- 스튜던트 t분포는 집단 3개 이상은 검정이 불가 -> F 분포로 검정
- 집단간의 분산을 다룬다.
- 분산 분석에 주로 다룬다
- 집단 간 분산 / 집단 내 분산
6. 가설 검정(test) - p value
- 내가 세운 가설이 통계적으로 유의한지 살펴보는것
- 가설 종류
귀무가설 : 뻔한 가설, 기각이 목표
대립가설 : 귀무가설에 대립되는 가설, 채택이 목표(귀무가설은 그럴 가능성이 없어 대립 가설이 맞아)
- 검정 순서
귀무가설, 대립가설 설정 -> p value 구한다 -> p value에 의해 가설의 채택/기각 여부를 결정
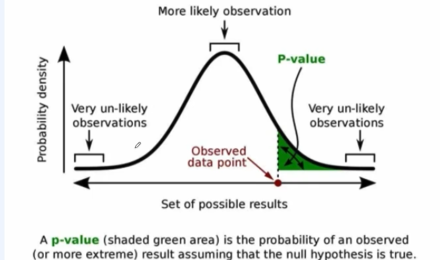
예시) 대립 가설 입장 - p value의 위치로 보아 귀무가설은 거의 발생하지 않아 그래서 대립가설을 채택해줘
- 검정
단측 검정(one-tailed test) : 한 방향성으로 가능성이 크다고 생각될때 - (예시) 구매력 비교 : 20대 < 30대
양측 검정(two-tailed test) : 방향성은 모르겠지만 차이가 있다고 생각될때 - (예시) 구매력 비교 : 30대 != 다른 연령대
- 주의점
: 잘못 결론을 냄(어떤 오류냐에 따라 도메인에 따라 크리티컬함이 다름)
제 1종 오류 - 귀무가설이 옳은데, 기각이 된 경우 (설레발)
제 2종 오류 - 귀무가설이 옳지 않은데, 채택이 된 경우 (믿는 도끼에 발등 찍힘)
6-1. t 검정(t test)
: 스튜던트 t분포를 사용한 통계적 검정 방법
- 배경
모집단의 분산이나, 표준편차를 알 수 없음
두 모집단이 있음
귀무가설(두 모집단에 평균 간의 차이가 없다), 대립가설(두 모집단에 평균 간의 차이가 있다)
- t 값(t value)
두 집단의 차이의 평균을 표준 오차로 나눈 값
- 기각역
t 값이 위치하는 범위

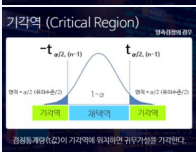
- t 검정 등분산성 검정
levene - p value 가 0.05 보다 크면 귀무가설 채택
ttest_ind - statistic이 0에 가까울수록 유무의한 차이가 없기때문에 귀무가설 채택, pvalue가 0.05보다 크면 귀무가설 채택
6-2. 분산 분석(ANOVA, Analysis of variance)
: 3개 이상의 다수 집단을 비교할때, 사용하는 검정방법
: F 분포
: 등분산성 가정 집단내 분산이 서로 비슷한가 비교가 가능해야한다.
- 검정 순서
Omnibus F 검정 : F값이 큰가? 차이가 있는가? - (예시) 사과를 키운다. 물과 햇빛간의 영향을 분석
post hoc 검정 : 구체적으로 얼마나 차이가 나는가? - (예시) 구체적인 차이
- anova 검정
f_oneway - Ominbuf F 검정
pairise_tukeyhsd - post hoc 검정, 사후 분석은 가설 검정을 많이 할수록 1종 오류가 발생할 수 있음
6-3. 카이제곱검정
: 카이제곱분포를 이용해서 검정을 한다
: 독립성 검정(두 변수는 서로 연관성이 있는지?)
- (예시) 귀무가설 : 유저 a 군과 b 군이 c 페이지 진입하는 것은 관련이 없다
- (예시) 대립가설 : 유저 a군과 b 군이 c 페이지 진입하는 것은 관려이 있다.
: 적합성 검정(실제 표본이 내가 가정한 분포와 같은가?)
: 동일성 검정(두 집단의 분포가 같은가?)
- 카이제곱검정 순서
1. 기대값을 구한다
- (예시) 기대값만큼 c 페이지에 진입해 줘야 함
2. 카이제곱을 한다(관측값 - 기대값의 제곱 / 기대값)
3. 2번 합쳐 전체의 카이제곱 값을 구한다
4. 카이제곱의 자유도를 구한다
- 카이제곱 검정
chi2_contingency(observed = 관측 dataframe) : 0.05 보다 크면 귀무가설 채택
'FastCampus UpStage AI > 통계' 카테고리의 다른 글
| FastCamPus X Upstage AI 5기 Statistics(통계학) 강의 (0) | 2024.10.11 |
|---|---|
| 기초 통계량 - 데이터 분포 이해 (분산도) (0) | 2024.10.08 |
| 기초 통계량 - 데이터 분포 이해 (대푯값) (0) | 2024.10.08 |